Journal of Neuroscience paper: “Age-Related Changes in 1/f Neural Electrophysiological Noise

October 1, 2015 by Bradley Voytek

Alright! Right on the tail of the publication of my Nature Neuroscience paper from my first post-doc with Mark D'Esposito is my latest paper in the Journal of Neuroscience from my second post-doc with Adam Gazzaley (PDF here). This one, “Age-Related Changes in 1/f Neural Electrophysiological Noise,” is yet another paper of mine that was published after getting rejected from journal that ultimately published it.

I'm really happy with this paper, as it's the culmination of a lot of musing, frustrations with the literature, and analyses made slower and more difficult by new parenthood. (It turns out, baby-induced sleep deprivation reduces my analytic and computation abilities.)

The genesis for the ideas in this paper came from when I first joined the Gazzaley lab. Adam is an expert in age-related cognitive changes (like his famous aging/training Nature paper from a few years back!) When I joined the lab I was interested in aging as a natural, non-pathological extension of my PhD work looking at post-stroke cognitive compensation. So I began to read about the neurophysiological basis of age-related cognitive decline, and one theory that kept popping up was the "neural noise" hypothesis.

What struck me, however, was the lack of a formal definition of "noise," especially in regards the biophysical/computational properties of neurons. Now of course there's a great deal we do not know, but I've built my research career around the role that neural oscillations play in coordinating information transfer between regions. One idea that has strong supporting evidence in this regard is that oscillations influence the timing and temporal probability of neuronal spiking, and that this is a plausible method for interregional information transfer in the brain.

Starting from this, I reasoned that a "noisier" system would have more spikes randomly distributed in time, relative to a carrier oscillation. Here's what that would look like:



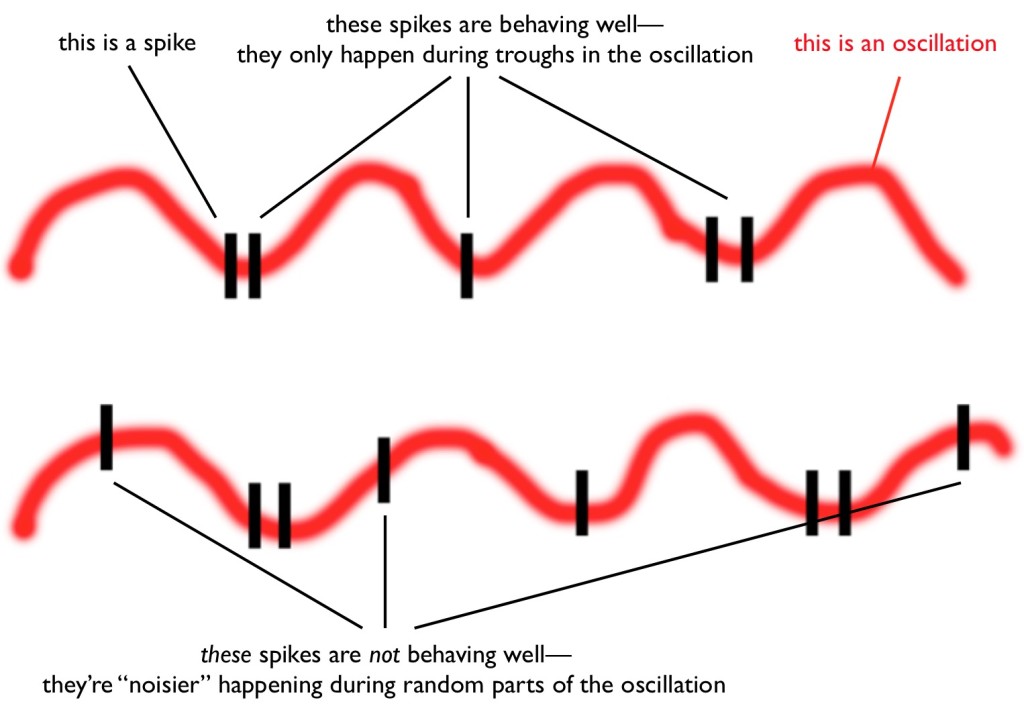
That's seriously it. That's where the idea started. The trick is, what data, if any, do we have from humans that we can use to measure that "noisiness"?

As we state in the paper:

If the neuronal population is highly correlated (a large number of spikes all occur relatively simultaneously, with few aberrant units spiking at times different from the population mode), then the aggregate local field potential (LFP) 1/f slope will be more negative. As the units within the population spike relatively asynchronously, the LFP 1/f slope will be flatter. Within this framework, age-related increases in neural noise would result in desynchronized spiking activity, reflected by a flatter power spectrum.

This all has to do with different "colors" of noise in time series of data, and even now in my lab we're beginning to suspect is far too simplified of an account. But it was a starting place.

As an aside, my lab's gotten so far down the "biophysical basis of the LFP" rabbit hole that even things I wrote just a few months ago on this topic (see my "neural jazz" post), seem far too oversimplified, or even wrong. If this kind of stuff interests you, feel free to drop me an email and/or check out my lab's posters at SfN!

From all of this, we began with a noise measure taking from a group of 15 of our invasive electrocorticography (ECoG) patients spanning an age range from 15 to 53 years old. Annoyingly, a reviewer kept arguing with us that this age range somehow didn't constitute "aging," which to be frank is still an argument I don't fully understand.



By definition, given our conceptualization of noise, the more random spikes occurring during different parts of the oscillation should decrease spike-field coupling, which we think we can measure in ECoG via phase-amplitude coupling (PAC). As predicted, the older the person, the flatter their spectral slope and the lower their PAC:



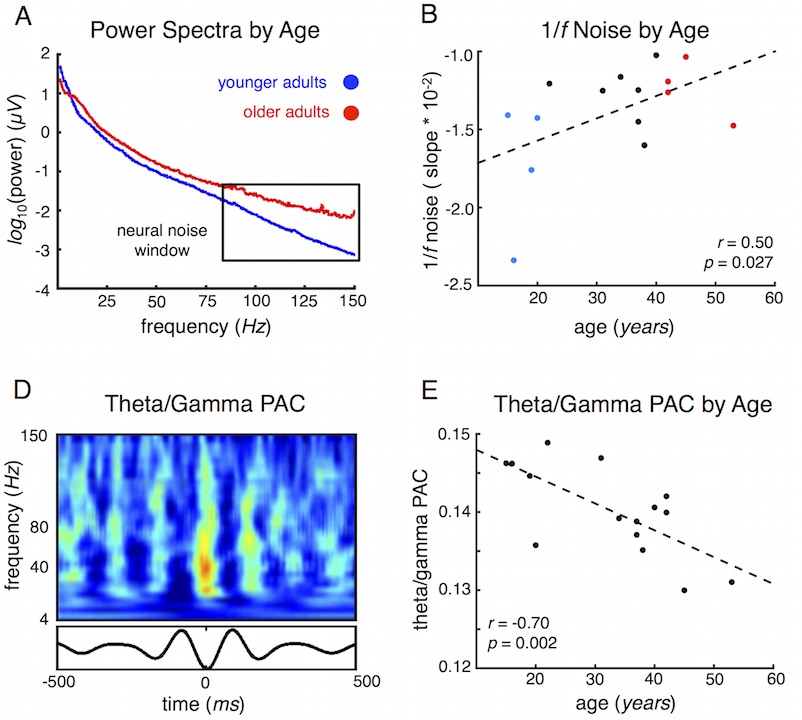
Amusingly, everyone--from my coauthors to the reviewers--came back asking how we knew this was a valid measure of noise (which is a fair point!) So we ended up building a full (simplistic) computational model of the relationship between spiking and oscillations to simulate the LFP and we found the same result!

And all this extra work ended up getting axed from the paper because the reviewers then came back and said, essentially, "neat! But this muddies the paper."

::sigh::

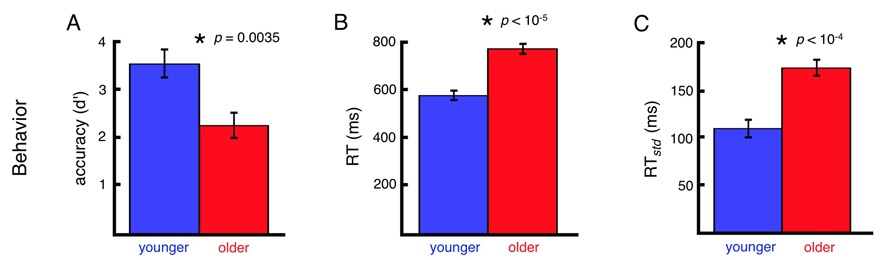
The interesting thing about this 1/f effect is that, if it's strong enough, it should even be visible at the level of scalp EEG. So we checked using a cohort of younger (20-30 years) and older (60-70 years) adults performing a visual working memory task. (Apparently this is a "real" aging sample, by the way.) As has been repeatedly show, the older adults showed lower working memory performance, with slower and more variable response times:



Now, the first time I plotted the power spectra and saw the outcomes below, I about lost it. These are the rare moments in science where you feel like, holy shit, maybe we're actually onto something here!



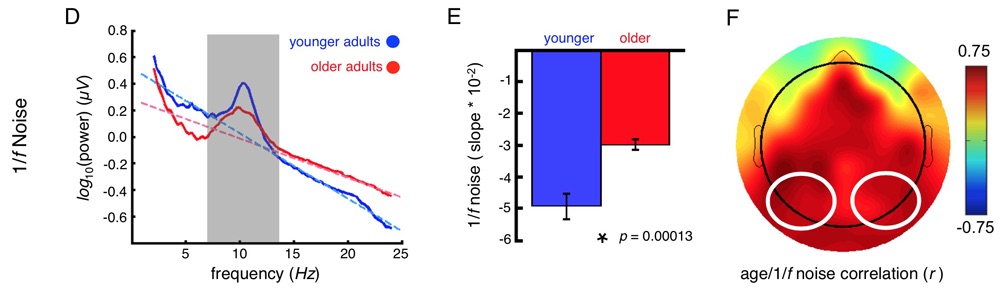
Amazingly, these 1/f slope differences were striking, and clearly discernible in our data, with older adults showing flatter (noisier) spectral slopes. These age-related slope differences had a spatial topography in non-invasive EEG, showing the strongest effects in visual and frontal regions during this visual working memory task.

I was so struck by this finding (and skeptical!), that I actually emailed a friend in the EU who I knew had an EEG aging dataset and asked them to just send me the average power spectra for the younger and older adults. And they showed the same pattern.

Within our data, these slope differences between younger and older adults also seem to mediate the age-related working memory deficits.

Internally in my lab, we've since replicated the age/slope finding. In fact, if you've got some EEG data laying around with younger and older adults, I'd be happy to show you how to do these analyses! You may get a neat aging/noise/cognitive paper out of it!

The ideas that formed this paper really changed the course of my research and my lab. We've gotten much more into computational modeling of oscillations as a communication system, neural noise, and so on. We've also gone deep into what the 1/f signal means, where it comes from, and how it relates to oscillations and spiking. This can be summarized from a section of the Discussion, with which I'll close this post:

We argue that, by considering the entire power spectrum as a unified statistical representation of the signal rather than examining semiarbitrary frequency sub-bands, age-related low-frequency power decreases and high-frequency power increases underlie the same phenomenon: increased 1/f noise causing a flattening of the power spectrum.