Interpreting the Electrophysiological Power Spectrum

August 24, 2015 by Richard Gao

(This post is written by Richard Gao, Voytek Lab PhD student in Cognitive Science and author of the target paper, "Interpreting the Electrophysiological Power Spectrum," published in the peer-reviewed, student-focused "NeuroForum" mini-review section for the Journal of Neurophysiology.)

This short article reviews some of the recent experimental data and simulation works done on the electrophysiological power spectrum (or power spectral density, PSD), and proposes a simple addition to the currently accepted inverse power law model of the PSD. What we find really cool about our new model is that it takes a purely mathematical description of neural signal PSDs, and adds to it a mechanistic component that explains recent empirical observations in human neurophysiological experiments, thus linking cellular level physiological processes to macroscopic measurements and cognitive behavior, from which we are able to make new predictions for future experiments to validate. Skip the first two sections if you are well-versed in systems neuroscience and Fourier Transforms, and skip the third one if you know about neural power spectrums and just want to read about findings in my new paper.

Background – What is Electrophysiology?

One of the ways our brain cells (neurons, specifically) communicate with each other is through electrical signaling, somehow giving rise to our cognition and consciousness. So if you stick a very precise voltmeter on the surface of your skull (EEG: electroencephalogram), on the surface of your brain (ECOG: electrocorticogram), or into the brain tissue itself (LFP: local field potential), you will record fluctuating electrical activity (electrophysiology), much like how you measure a battery. More miraculously, this fluctuating electrical activity has been found to correlate to changes in behavior and mental states of a living person, and neuroscientists have been taking advantage of this relationship for decades, gaining insight on how the brain and the mind are related. The raw recorded signal (time domain), however, does not look to be very informative, as they are composed of squiggly lines that seem no different from one moment to the next (except for a few situations, like if you are asleep or very dead). So we’ve borrowed tools from electrical engineering to transform the data while keeping the information intact, much like rotating an object to reveal key visual features so we can better determine what it is, or going from base 2 to base 10 (is 101010 the meaning of life?)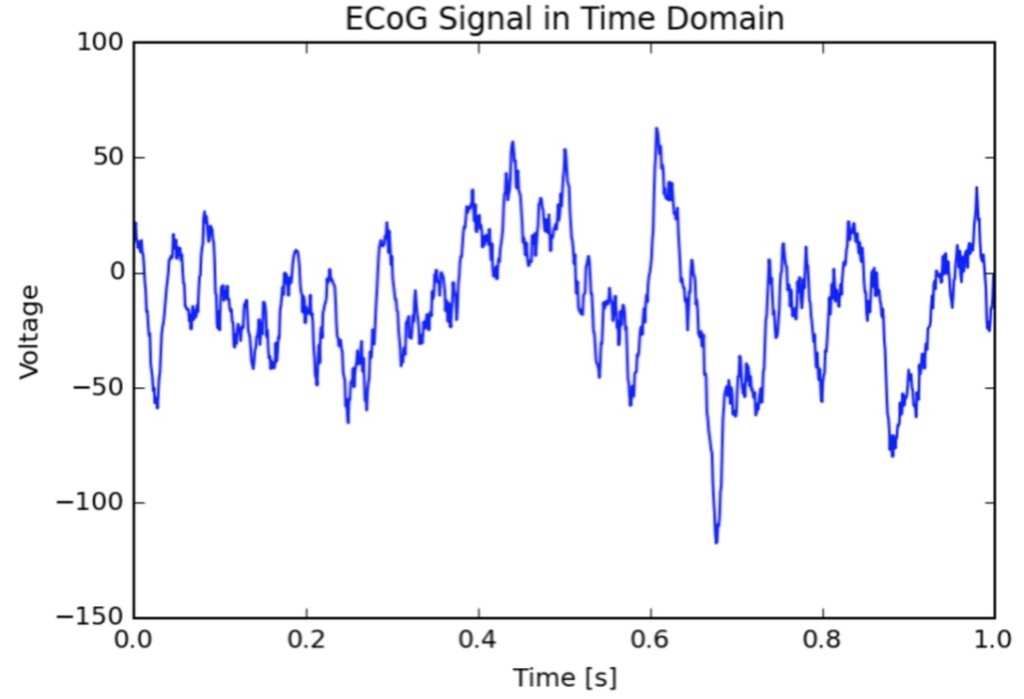

Squiggly lines otherwise known as an electrophysiological signal (ECoG, in this case).

Fourier Transform – Breaking Down the Chords

The tool in question is called the Fourier Transform, and it is one of the most useful ideas born from mathematics to become pervasive in all aspects of our lives. In essence, it separates a single signal varying in time into its (sinusoidal) frequency components, measured in cycles per second (hertz, Hz). For example, when you hear a piano chord, it is just a continuous stream of pressure waveforms that hits your eardrum, but your ear canal performs the equivalent of a Fourier Transform to separate the chord into its constituent notes, such as A (440Hz), C (261Hz), and G (392Hz). How loud each of the frequency components is makes up the PSD. Note that, technically, a power spectrum and power spectral density are two separate things, but for our purposes, we use them interchangeably. For a more in-depth exposition of Fourier Transform and the PSD, consult Wikipedia and many great tutorials on the web. Or check out our awesome in-house iPython tutorial, built by our very own Torbenator.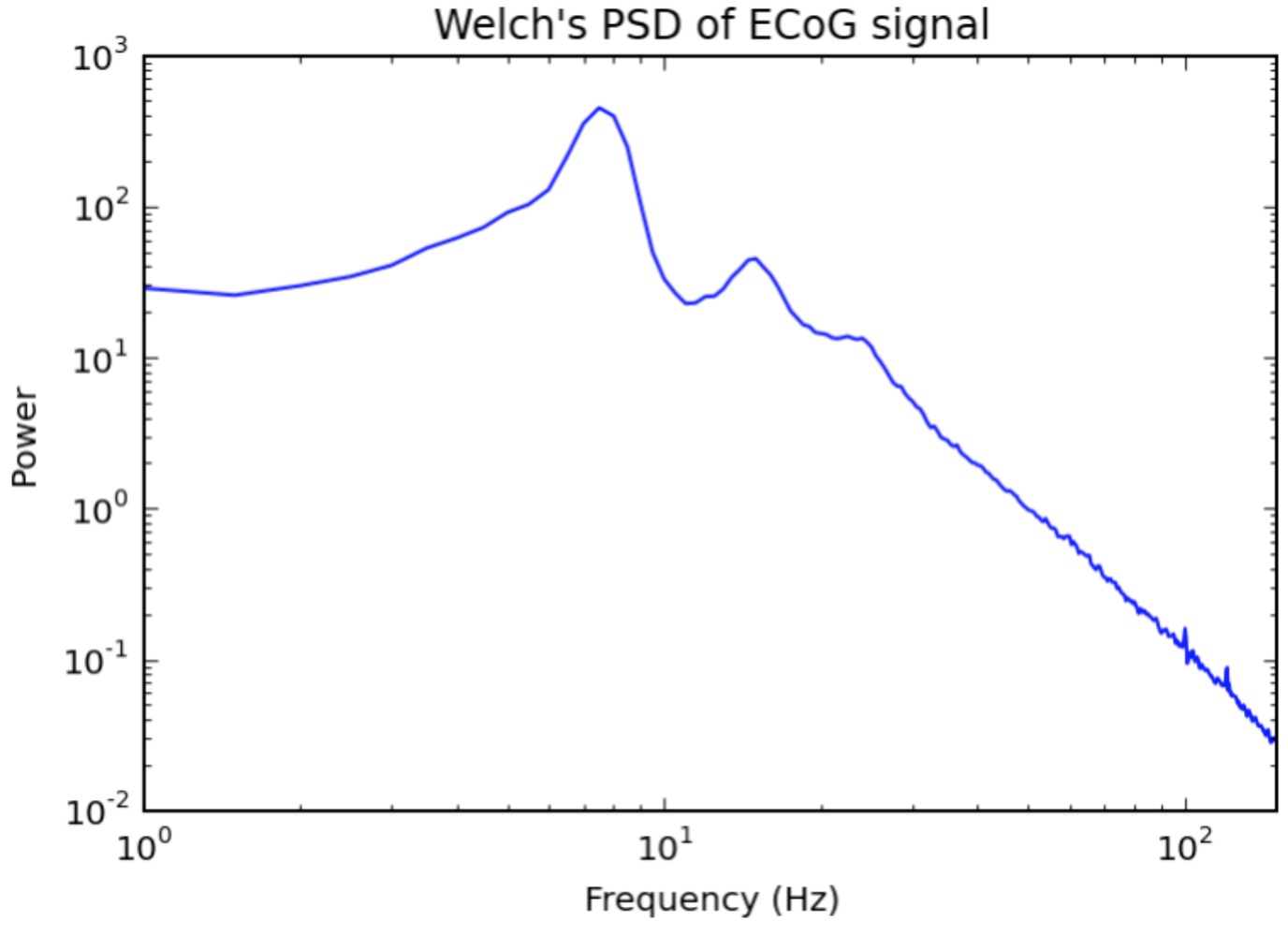

PSD of the previously shown squiggly signal (in log-log) – much nicer, no?

Power Law – 1/f Electrophysiological PSD

Back to our electrophysiological signal: the PSDs of electrophysiological signals are usually much more informative than the raw time domain voltage traces themselves. This is because specific oscillations are better represented in the PSD. In the PSD figure above you can see prominent peaks around 8Hz and 15Hz, which are a couple of popular frequencies in the neural oscillations research community, correlating to a vast range of behavioral variables such as attention, relaxation, and motor control, just to name a few. You might also notice that the high-frequency portion of the PSD (>30Hz) is surprisingly regular (linear), with a very consistent slope. This downward sloping line signifies that the signal power decays as a function of its frequency. Analogously, imagine pressing all the keys on a piano at the same time, only rather than pressing them all with the same strength, you press the lower keys with a much higher force than the higher keys, and the force you apply is a mathematical function of how high the note is. The function, in this case, is described by an inverse power law, or P(f) = Af^χ, where χ is a negative number. When plotted in log-log space, we see that logP(f) ~ logA + χlogf, hence the downward sloping line as a function of frequency (remember, χ is negative).

Rotation of the PSD – When Power Law is Not Enough

The observation that the PSD follows an inverse power law is the main topic of our new paper. Previously, we have been satisfied with the mathematical description of the PSD in the form of P(f) = Af^χ, with oscillatory bumps riding on top. Many theories were put forth to explain this “power law” behavior of the PSD, though it remains largely a descriptive and mathematical model, instead of a mechanistic one. More importantly, experimental data from other labs have implicitly suggested that the strict power law model is incomplete in several ways. Given the model, one would expect that the rotation of the PSD to be reasonable (even if mechanistically undetermined) through a changing of the exponent χ, much like how a seesaw rotates around a fixed point, under certain mental states.

However, recent human ECoG data shows an apparent rotation of the high frequency portion of the PSD independent of the lower frequency components (like having a hinge somewhere on the seesaw) during mental engagement, which cannot be captured by the power law alone. In addition, when the PSD rotates, it does not rotate about a fixed axis of 1Hz, as would be predicted by the power law equation. In fact, the frequency of rotation decreases as the PSD becomes flatter, which is the same as the seesaw sliding away from the fulcrum the more balanced it becomes.

Neural Spiking Can Tip the PSD – Proposed Model

We were able to account for the discrepancies between the current model and the observed data by adding a constant term, B, in the power law equation, i.e., P(f) = Af^χ + B. The constant in the frequency domain corresponds to a signal with (roughly) equal power across all frequencies, which, conveniently enough, is generated by a summation of many Poissonic (randomly) spiking neurons, each contributing a tiny impulse-like signal that is summed and registered by the recording electrode far away. This Poissonic signal is in addition to the underlying power law signal that is often cited to be synaptic (slower signals between neurons) in origin. Due to the nature of the underlying inverse power law PSD, the constant signal affects the low power (high-frequency) portion of the PSD much more than the high-power portion, effectively rotating only the high-frequency parts of the PSD, as recently empirically observed by Podvalney and colleagues. In addition, increasing firing rate of the Poissonic population translates to a flatter PSD, and the frequency of rotation decreases as the PSD slope tends towards 0. In this way, we were able to explain previous experimental findings with a simple addition to the existing model. Furthermore, it goes beyond a simply descriptive model of the PSD, and provides a mechanistic origin for a different, but related, signal that acts separately from the underlying power law PSD. Armed with this proposition, we can then ask experimentally testable questions, such as which mental states increase or decrease neural spiking and how are the two signals related. As always, a picture is worth a thousand words, better yet is a live demonstration, so check out our iPython Notebook tutorial (with a playable widget).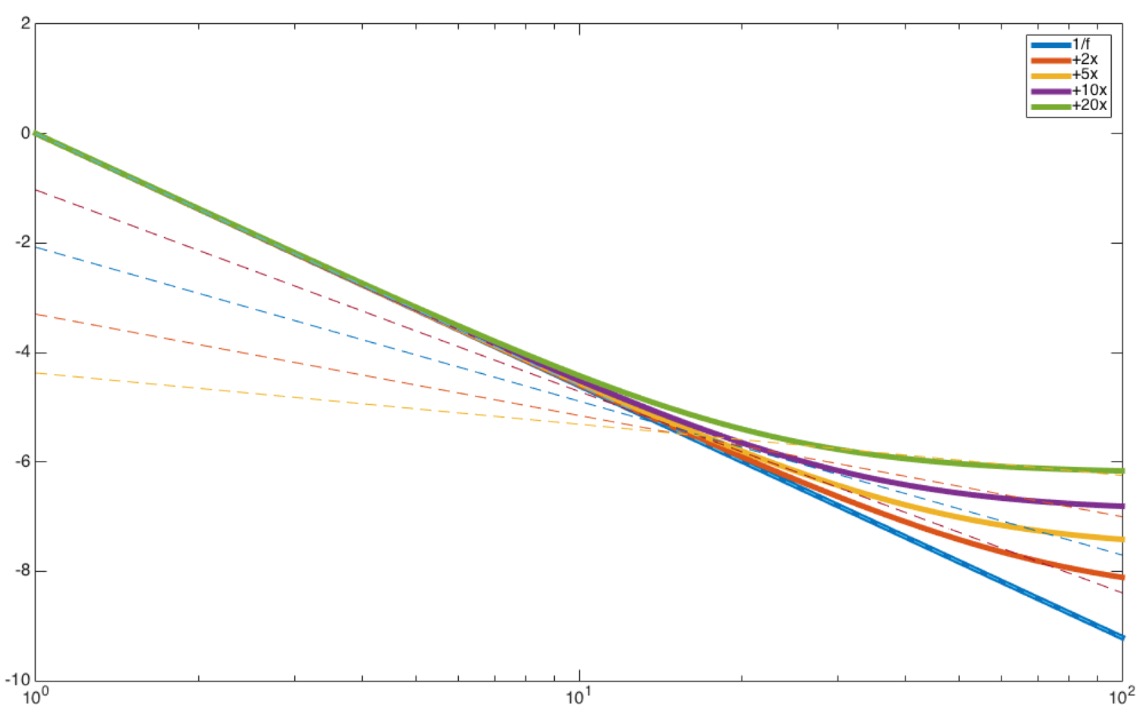

Increasing the firing rate of a Poisson spiking neural population rotates the PSD in log-log.

Ending Remarks & Limitations

To conclude, we’d like to point out a few potential issues with the new model. Firstly, it is debatable whether, from an electronics point of view, neural spiking (action potentials) can be recorded by a large electrode (such as ECoG). To this end, we are not claiming to record single spikes, but an aggregate of many, many neurons, which ends up looking like fuzzy noise from really far away. The power of this fuzzy noise signal corresponds to how much the neurons are firing, which is possible to pick up using macroscopic electrodes. Secondly, neurons are certainly not all firing perfectly randomly (Poissonic), as our simulation currently does. However, it is largely accepted that, although firing rate varies depending on task and condition, individual neurons do fire in a Poisson-like manner (sort of). This naturally leads to the question of how different neuron firing patterns influence the PSD, which is under active investigation in the Voytek lab. Finally, while the constant term was shown to be Poissonic spiking in nature, the power law PSD was still, if you will, hand-waved over to be “synaptic”. One might argue that changes in slope could be modeled as a wide bump in the PSD, similar to how narrowband oscillations are currently modeled. Once again, this is under active investigation in the lab and stayed tuned for future publications.

As always, comments and suggestions are very welcome, as well as downloading our code to play with the simulations. Thank you for reading.

Gao, R. (2015). Interpreting the Electrophysiological Power Spectrum Journal of Neurophysiology DOI: 10.1152/jn.00722.2015